Ist der Tonraum flach oder gekrümmt?

Dieser Aufsatz richtet sich an Schülerinnen und Schüler der Abiturstufe, die sich für Mathematik und Musik interessieren. Anhand eines Theorieentwurfs zur Erforschung des Denkens in Tönen, wird hier der Versuch einer leicht verständlichen Einführung in ein  spannendes Untersuchungsfeld unternommen. Anstelle eines verlässlichen, nach didaktischen Gesichtspunkten geordneten Kanons an Fachwissen wird hier eine kleine Kostprobe wissenschaftlichen Argumentierens geboten. Es ist noch offen, wie sich einzelne Argumentationslinien beim weiteren kritischen Ausbau der Theorie entwickeln werden. Der Aufsatz unterscheidet sich von einem wissenschaftlichen Fachbeitrag unter anderem in einer zurückhaltenden Zitatologie. Stattdessen wird von den Musiktheoretikern, manchen Musiktheoretikern, einigen Musiktheoretikern gesprochen, wenn es etwa darum geht, den Verbreitungsgrad von Auffassungen zu charakterisieren. Beim Bemühen um Vereinfachung ist dennoch darauf geachtet worden, viele Argumentationsalternativen wenigstens aufzuzeigen, wenn auch auf manche Verzweigungen bewusst verzichtet wurde. Die mathematische Seite der Theorie wurde auf ein Niveau reduziert, das sich jedem interessierten Leser erschließen sollte [1]. Zur Illustration verschiedener Details gibt es eine Sammlung klingender Geometrien, die mit dem Programm VisibleMusic studiert werden können [2]. 

Es geht um ein bisher ungelöstes Rätsel der Musiktheorie. Wir wollen es das Töne-Noten-Tasten-Problem nennen. Man sollte zwei Dinge vorwegschicken. Unter den Musiktheoretikern herrscht keineswegs Einigkeit darüber, ob es ein solches Problem überhaupt gibt, und wenn ja, ob es auch interessant genug ist, Zeit darauf zu verwenden. Die Hauptschwierigkeit besteht letztlich darin, es präzise zu formulieren. Es handelt sich sich um ein Problem, welches mit der Entwicklung der abendländischen Musik zu tun hat. Es zeigt sich unter anderem im Zusammenhang mit den Stimmungsproblemen von Tasteninstrumenten und überhaupt bei Intonationsfragen. Aber es ist ja oftmals so, daß ein Problem woanders sitzt als sich zeigt. Etwas genauer formuliert: Unter Musiktheoretikern gibt es die verbreitete Annahme, daß bestimmten musikalischen Tonbeziehungen ideale Frequenzverhältnisse der zu intonierenden Ton-Klänge entsprechen. Sobald man unter dieser Annahme aber versucht, für die Noten einer Partitur systematisch zu entscheiden, wie diese idealerweise zu intonieren wären, so stoßt man ständig auf Schwierigkeiten, die daher rühren, daß einunddieselben Noten Träger verschiedener konkurrierender Tonbeziehungen sind. Die ausübenden Musiker und Musikhörer scheinen diese Schwierigkeiten indes nicht zu kennen; und wenn doch, so sind sie offensichtlich in der Lage, sie zu meistern. Es gibt gute Gründe für die Annahme, daß sich hinter diesem scheinbaren Widerspruch zwischen Theorie und Praxis, verborgene Eigenschaften unseres Denkens in Tönen offenbaren.

1 Was ist ein Tonraum?

Mit dem Begriff des Tons verbinden sich mindestens drei verschiedene Ebenen, die man auseinanderhalten sollte. Nehmen wir an, jemand hört den letzten Ton seiner Lieblingsmelodie. Aus der Sicht eines Akustikers bedeutet dies, daß diese Person von einer Luftschwingung Notiz nimmt. Für einen Hörpsychologen bedeutet es, daß die Person eine Tonhöhenempfindung hat. Und für einen Musiktheoretiker bedeutet es, daß die Person in ihrer Tonvorstellung einen bestimmten Tonort aufsucht: eine Position in einem abstrakten Tonsystem, in welchem auch die anderen Tönen ihrer Lieblingsmelodie geeignete Positionen einnehmen. Für unsere Argumentation ist die letzte der drei Ebenen ausschlaggebend. Tonbeziehungen entstehen in unserem Modell durch geeignete Fortschreitungen von Tonorten zu anderen Tonorten. Es ist aber wichtig, auch die anderen beiden Ebenen zu betrachten. Für viele Forscher besteht das Töne-Noten-Tasten-Problem deshalb nicht, weil sie der Meinung sind, daß es sich dabei lediglich um Effekte handelt, die beim Übergang von einer dieser Ebenen in eine andere auftreten. Gerade über das Verhältnis von Wahrnehmung und Denken weiß man aber heute noch sehr wenig. Immerhin ist bekannt, daß unser Gehör kein unbestechliches Meßgerät ist, sondern sich in seiner Leistungsfähigkeit an die Musik anpaßt, die wir zu hören gewohnt sind. Man spricht von kategorischer Wahrnehmung. In Abhängigkeit von den Intervallen, die wir oft unterscheiden müssen, ist unser Unterscheidungsvermögen für Intervallgrößen ungleichmäßig entwickelt, und zwar durch Lernprozesse. Dies ist ein Hinweis darauf, daß sinnliche Wahrnehmung und Denken in der Musik eng miteinander interagieren. Manche Forscher scheuen sich jedoch, vom Denken in Tönen zu sprechen, weil ihnen die damit bezeichneten Phänomene als ein Bereich bloßer Spekulation erscheinen. Andererseits würde unser musikalisches Erleben aus der einseitigen Sicht der kategorischen Wahrnehmung das merkwürdige Bild einer zappelnden Kommode mit vielen Schubladen ergeben, die in einer gewissen Folge auf- und zuspringen. Etwas Mut zur Spekulation kann also nicht schaden, und eine Reihe von Theoretikern haben interessante Vorschläge gemacht, denen man nachgehen kann [3]. An die Stelle der zappelnden Kommode stellen wir ein geometrische Bild vom Tondenkens, nämlich das eines Tonraumes, in welchem das Denken durch Schritte in verschiedene Richtungen von bereits erreichten Tonorten zu anderen Tonorten gelangen kann.  

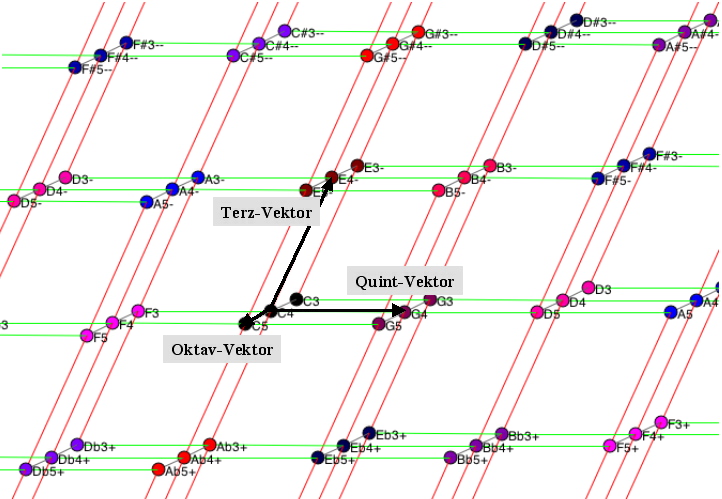
Geometrische Vorstellungen vom Tonsystem findet man in vielen Büchern zur Harmonielehre. Verbreitet ist die Anordnung der Tonorte in einem dreidimensionalen Gitter, das von den drei Intervallen Oktave, Quinte und Terz aufgespannt wird (siehe Abbildung 1). Dahinter steht die Idee, daß es elementare Tonbeziehungen gibt, aus denen sich komplizierte zusammensetzen. Die drei Intervalle Oktave, Quinte und Terz gelten für die Musiktheoretiker deswegen als elementar, weil ihnen auf der physikalischen Ebene sehr einfache rationale Frequenzverhältnisse entsprechen und sich die prominenten Dur- und Molldreiklänge aus ihnen zusammensetzen. Die Frequenz einer Schwingung ist die Anzahl der Wiederholungen einer periodischen Grundbewegung pro Sekunde (z.B. der Hin- und Herbewegungen einer Stelle auf einer gezupften Saite oder eines Luftteilchens, das davon angeregt wird). Bei der Erklärung musikalischer Intervalle vergleichen die Musiktheoretiker je zwei Schwingungen und betrachten deren Frequenzverhältnisse. 

	Beim Frequenzverhältnis 2 : 1, spricht man vom Oktav-Intervall.
	Beim Frequenzverhältnis 3 : 2, spricht man vom Quint-Intervall.
	Beim Frequenzverhältnis 5 : 4, spricht man vom (reinen) Terz-Intervall.

Dabei spielt die folgende hörpsychologische Tatsache eine Rolle: Wann immer wir zwei Paare von Schwingungen hören, deren Frequenzen dasselbe Zahlenverhältnis bilden, erscheint uns der Abstand der dabei sinnlich empfundenen Tonöhen als gleich. Daraus schließt man das sogenannte Fechnersche Gesetz: Unabhängig von den konkreten Frequenzen entspricht der Vervielfachung von Frequenzen eine Addition der empfundenen Tonhöhenabstände. Wie entsteht daraus ein Tonraum-Modell? Man postuliert zunchst einen AusgangsTonort und versteht dann Oktav-, Quint- und Terz-Fortschreitungen als Fortschreitungen unabhängige Richtungen, weshalb der gesuchte Raum folglich dreidimensional sein muß. Warum sollten diese Richtungen unabhängig voneinander sein? Dazu kann man mathematisch die Begründung anführen, daß 2, 3 und 5 Primzahlen, also teilerfremd sind. In Bezug auf ein Denken in Tonorten muß man dieses Argument jedoch mit allergrößter Vorsicht behandeln, denn es würde implizit unterstellen, daß wir in unserer Tonvorstellung imaginierte Schwingungen zählen. Wir begnügen uns lieber mit der Tatsache, daß die Musiktheorie zu einer räumlichen Metapher des Tondenkens gelangt ist. In Abschnitt 4 werden wir über alternative Argumente zugunsten einer solchen Auffassung nachdenken. Die Abbildung 1 zeigt den dreidimensionalen Eulerschen Tonraum.

Abbildung 1: Der Eulersche Tonraum

Ein Phänomen mit wichtigen Implikationen ist das der Oktavidentifikation. Damit ist gemeint, daß man Tonorte im Eulerschen Tonraum, die man durch Schritte in Oktavrichtung erreichen kann, identifiziert. Bei dieser Auffassung werden die identifizierten Tonorte auf einer höheren Abstraktionsstufe als einundderselbe Tonort in einem nur noch zweidimensionalen Raum angesehen. Dabei kann ein Theoretiker entweder die Oktavidentifikation einfach als gegeben erachten und von vorn herein jene abstrakteren Tonorte als die eigentlichen Tonorte ansehen, oder er kann die Oktavidentifikation innerhalb seiner Theorie als ein eigens zu behandelndes Phänomen betrachten. Wir machen uns das Leben etwas leichter und folgen der verbreiteten ersten Auffassung. Mathematisch bedeutet dies, daß wir einen zweidimensionalen Raum von Tonorten betrachten, der vom Quint-Vektor und vom Terz-Vektor aufgespannt wird. Wir sprechen dabei vom Eulernetz. Man findet es in vielen Büchern zur Harmonielehre (siehe Abbildung 2). Zur Erinnerung: Vektoren sind bestimmt durch eine Richtung und einen Betrag.

Im Laufe dieses Beitrages wird es darum gehen, dieses Modell zu modifizieren, um dadurch das Töne-Noten-Tasten-Problem zu lösen. Zuvor wollen wir kurz darüber nachdenken, was es überhaupt bedeuten kann, ein geometrisches Modell für das Tondenken zu verwenden.

Für Mathematiker ist es heute ganz selbstverständlich, sich mit abstrakten Räumen in soundsoviel Dimensionen und den merkwürdigsten Eigenschaften zu beschäftigen.

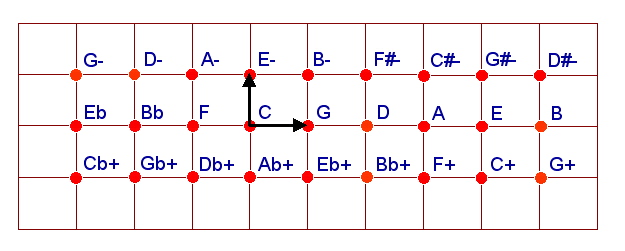
Abbildung 2: Das zweidimensionale Eulernetz

Aber warum tun sie das, und was bedeuten diese Räume? Durch die Erfahrungen, die wir mit unseren Körperbewegungen und Sinneseindrücken von Kindesbeinen an machen, gewinnen wir eine vertraute Anschauung vom dreidimensionalen Raum. Dieser Raum ist für uns einfach da. Die Entstehung vieler älterer und jüngerer sprachlicher Ausdrücke und redebegleitender Gesten zeigt, daß wir bei der Erschließung anderer Erfahrungsbereiche ebenfalls von der räumlichen Anschauung Gebrauch machen. Wenn wir beispielsweise von hohen und tiefen Tönen sprechen, so kann man das eine räumliche Metapher nennen. Metaphern sind ein So-Tun-Als-Ob. Man überträgt etwas noch unvollkommen Verstandenes in einen vertrauten Bereich, um dort damit besser operieren zu können. Insofern stehen dahinter so etwas wie Gedankenexperimente. Die im Beispiel genannte Metapher der Ton-Höhe ist offenbar eine sehr gute Wahl, denn nach dem Fechnerschen Gesetz handelt es sich nicht nur um eine reine Anordnung von möglichen Hörempfindungen längs einer Achse, sondern wir können offensichtlich Empfindungsdifferenzen bilden und diese zueinander addieren, ganz so wie wir mit Elle oder Zollstock zu hantieren gewohnt sind.

Aber auch die Tätigkeit der Mathematiker hat mit Gedankenexperimenten zu tun. In der Geometrie denken sie sich Symbole aus für die Punkte, Richtungen, Abstände und Winkel und führen damit verschiedene Operationen aus - und zwar zunächst anstelle der vertrauten Operationen, die die räumliche Erfahrung ausmachen. Anstatt beispielsweise einen Kopfstand zu machen, multiplizieren sie einfach die x-Koordinate (Rechts-Links-Richtung) und die z-Koordinate (Oben-Unten-Richtung) aller Punkte mit -1. Sind solche Gedankenexperimente auch räumliche Metaphern? Sie scheinen eher das Gegenstück davon zu sein. Der abstrakte Euklidische Raum mit seinen Transformationen erlaubt es uns, die vertraute Anschauung zusätzlich in der Metapher des mathematischen Modells zu verstehen. Angewandte Modelle sind ebenfalls Metaphern. Allerdings besteht die Mathematik keineswegs nur aus der Aufstellung und Anwendung isolierter Modelle. Die Eigenständigkeit der Mathematik äußert sich darin, daß viele Gedankenexperimente nicht in der direkten Auseinandersetzung mit den außermathematischen Anwendungen vollzogen werden, sondern zu einem großen Teil von innermathematischen Überlegungen ausgelöst werden. Erstaunlich ist, daß dabei hin und wieder brauchbare Modelle ür außermathematische Phänomene zu Tage gefördert werden, die im Sinne der vertrauten Anschauung eher ungewöhnlich sind.

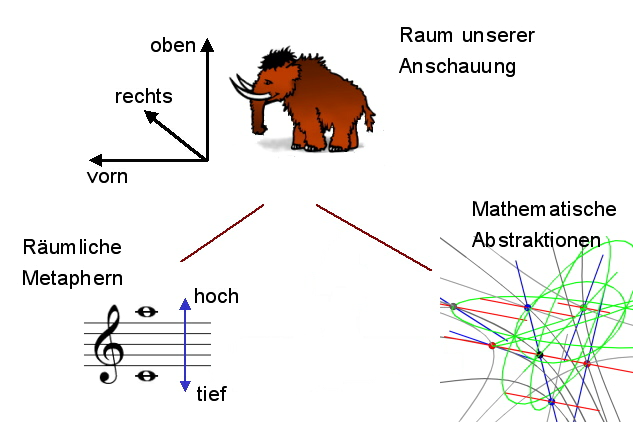
Abbildung 3: Räumliche Metaphern und abstrakte Räume als Gedankenexperimente

Daß wir uns über solche Modelle wundern, mag daran liegen, daß wir den Übergang von einer räumlichen Metapher zum mathematischen Modell des Euklidischen Raumes mit kartesischen Koordinaten als Selbstverständlichkeit ansehen, und dabei vergessen, daß sich räumliche Metaphern der vertrauten räumlichen Anschauung lediglich bedienen, um einen anderen Erfahrungsbereich besser zu verstehen. Bei dieser Verkettung kann es leicht passieren, daß in ein mathematisches Modell mehr Annahmen einfließen als nötig sind. 

Ob sich das Modell des gekrümmte Tonraumes, um das es in diesem Beitrag geht, für die Musiktheorie als brauchbar herausstellt, ist noch eine offene Frage. Auf jeden Fall ist er unanschaulich im Sinne unserer vertrauten räumlichen Erfahrung.

Fragen wir uns also, welche Gründe das Eulernetz rechtfertigen, so wie wir es oben kennengelernt haben? Einige Theoretiker benutzen es vielleicht nur als Gedächtnisstütze, um für sich selbst einen geordneten Überblick über das Tonsystem zu haben. Da ihnen der Euklidische Raum am besten vertraut ist, läßt sich dagegen nichts einwenden.

Bei jenen Theoretikern, die das Eulernetz als Modell für eine räumliche Metapher des Tondenkens verwenden, muß man genauer herausfinden, was diese Metapher motiviert. Konkret geht es beim Eulernetz um die Frage, wie das Verhältnis von Tonhöhen und Tonorten verstanden wird. Ist die Tonhöhe untrennbarer Bestandteil oder eher ein selbständiger Vermittler des Denkens in Tonorten? Im ersten Falle unterstellt man, daß an jeden Tonort eine zugehörige mitgedachte Tonhöhe [4] gekoppelt ist. Die Addition von Tonvektoren würde dann mit der Addition von Tonhöhendifferenzen korrespondieren. Oder anders gesagt: Die Tonhöhe wäre eine lineare Funktion des Tonortes. Dies wäre ein plausible Rechtfertigung des Eulernetzes als Modell des Tondenkens. Wie wir gleich sehen werden, hat man dann aber das Töne-Noten-Tasten-Problem. Verzichtet man aber auf diese feste Koppelung von Tonort und Tonhöhe, so verschwindet auch die Notwendigkeit, das Fortschreiten von Tonort zu Tonort mit der Addition von Tonvektoren in einem flachen Raum zu beschreiben. 

2 Das Töne-Noten-Problem

Ein paar Grundkenntnisse in Notenkunde werden im folgenden vorausgesetzt, und erinnern wir hier an wenige elementare Fakten, die im folgenden wichtig sind. In Abbildung 2 sind die Tonorte des Eulernetzes mit Namen versehen, die Dich bestimmt an Notennamen erinnern. Auf der mittleren horizontalen Achse stehen von links nach rechts folgende Bezeichnungen: 

. . . Eb Bb F C G D A E B . . .

Die Punkte deuten an, daß sich der Tonraum nach links und rechts beliebig weit ausdehnt. Die sieben Namen F, C, G, D, A, E und B [5] bezeichnen die sogenannten Stammtöne. Ihnen entsprechen auf der Klaviertastatur die weißen Tasten. Doch Vorsicht: Es gibt noch andere Noten, denen ebenfalls weiße Tasten entsprechen, z.B. B# (in Deutsch His), E# oder Dbb. Das hat bereits mit dem Noten-Tasten-Problem zu tun. 
Jedem Tonort auf der mittleren Quintachse des Eulerschen Tonnetzes entspricht eine eigene Note. Wegen der Oktavidentifikation im Eulernetz ist damit in den Noten ein beliebiger Oktavausschnitt zu wählen, für den diese Aussage dann gilt. Die Abbildung zeigt 35 verschiedene Noten, denen 35 aufeinanderfolgende Tonorte auf der Quintenachse entsprechen. Eine weitere Fortsetzung nach links und rechts würde in den Noten zu praktisch kaum vorkommenden dreifachen B's und Kreuzen führen, wäre aber prinzipiell korrekt. Das Töne-Noten-Problem wird deutlich, wenn man erneut einen Blick auf das Eulernetz wirft. In jeder der anderen horizontalen Geraden, in denen man ebenfalls von rechts nach links in Quintschritten fortschreitet, sind die Tonorte mit denselben Namen  versehen, wie in der mittleren Quintenachse. Allerdings sind die jeweils übereinstimmenden Namen bei der jeweils nächsttieferen Geraden um 4 Schritte nach rechts verschoben. Außerdem werden den Namen der Tonorte oberhalb der mittleren Quintenachse Minuszeichen angehängt und denen unterhalb Pluszeichen. Die Anzahl der Minus- oder Pluszeichen entspricht dem Abstand (in Schritten) von der mittleren Quintachse. Was verbirgt sich hinter diesem Muster? 

Abbildung 4: Die Noten der Quintenreihe und ihre Namen. Die beiden Zeilen stehen hier lediglich aus Platzgünden untereinander. 

Erinnern wir uns an die Definition des Tonnetzes! Die Schritte in vertikaler Richtung [6] sind reine Terzen, denen das Frequenzverhältnis 5:4 enspricht. Die Namensverteilung im Eulernetz macht deutlich, daß die Notenschrift nicht unterscheidet zwischen Quint- und Terzbeziehungen. Wenn man vom zentralen Tonort C aus vier Quintschritte nach rechts macht, erreicht man den Tort E. Geht man hingegen einen Terzschritt nach oben, so erreicht man den Tonort E-. Beiden Tonorten E und E- entspricht dieselbe Note. Das hinzugefügte Minuszeichen zeigt an, daß die Tonhöhe der Terz (nach geeigneter Oktavversetzung um 2 Oktaven nach oben) um ein sogenanntes syntonisches Komma kleiner ist als die vierfache Quinte. Dabei handelt es sich um eine kleine Tonhöhendifferenz von etwa dem Fünftel eines Halbtons. Dahinter steht ein Frequenzverhältnis 81/80, denn

 . 

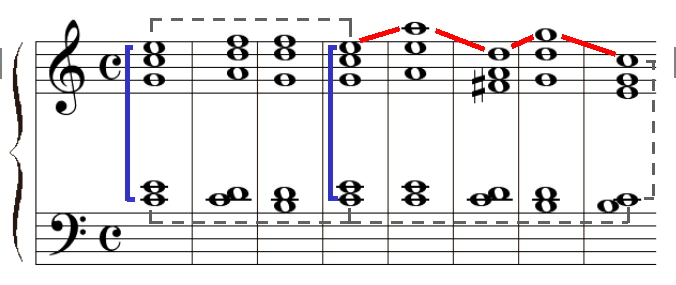
Wie schon eingangs erwähnt, äußert sich das Töne-Noten-Problem in konkurrierenden Tonbeziehungen, deren Träger einunddieselben Noten sind. Dazu betrachten wir nun zwei Beispiele. Das erste hat der berühmte Musikwissenschaftler Hugo Riemann in einem Aufsatz aus dem Jahre 1914 aufgeführt (siehe [L4]). Er hat es eigens so konstruiert, daß das Problem besonders deutlich wird: Das Beispiel bringt eine Folge von fünf Dreiklängen. Jeweils einer der Töne ist in der Oktave verdoppelt. Dadurch wird der Satz vierstimmig.

C - Dur-	A - Dur-	D - Moll-	G - Dur-	C - Dur-
Dreiklang	Dreiklang	Dreiklang	Dreiklang	Dreiklang

Dur- und Moll-Dreiklängen entsprechen im Eulernetz jeweils Dreiecke. Bei Dur-Dreiklängen gesellen sich zum Tonort des Grundtons dessen rechter und oberer Nachbar (Quint-Tonort und Durterz-Tonort). Bei Moll-Dreiklängen gesellen sich zum Tonort des Grundtons dessen rechter Nachbar (Quint-Tonort), sowie der untere Nachbar des Quint-Tonorts (Mollterz-Tonort). 

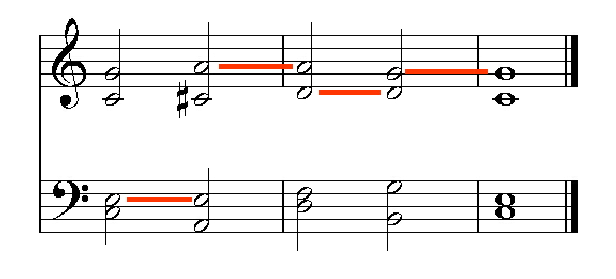
Abbildung 5: Beispielkadenz von Hugo Riemann, die das Töne-Noten-Problem verdeutlicht. 

Welche Tonbeziehungen lassen sich auf den ersten Blick aus dem Notenbeispiel ablesen? Wir machen zwei Beobachtungen: 

1.  Die Notationen des ersten und des letzten C-Dur-Dreiklanges sind identisch (bis auf die Dauern). Dadurch wird nahegelegt, daß die zugehörigen Tonorte identisch sind. 

2. In jedem Akkordschritt bleibt in jeweils einer der vier Stimmen eine Note liegen: Vom C-Dur-Dreiklang zum A-Dur-Dreiklang das E im Tenor [7], vom A-Dur-Dreiklang zum D-Moll-Dreiklang das A im Sopran, vom D-Moll- Dreiklang zum G-Dur-Dreiklang das D im Alt und vom G-Dur-Dreiklang zum C-Dur-Dreiklang das G im Sopran. Wenn man auch hier annimmt, daß jedesmal die Tonorte dieser Noten in beiden Akkorden identisch sind, ergeben sich jeweils Tonbeziehungen sowohl im vorausgehenden als auch im nachfolgenden Akkord: E ist die Terz im ersten C-Dur-Dreiklang und auch die Quinte im A-Dur-Dreiklang, dessen Grundton A auch die Quinte im D-Moll-Dreiklang ist, dessen Grundton auch die Quinte im G-Dur- Dreiklang ist, dessen Grundton auch die Quinte im letzen C-Dur-Dreiklang ist.  

 Wenn man sich lediglich an die zweite der beiden Beobachtungen hält, so ergibt sich im Eulernetz eine Wanderung in vier Schritten wie sie Abbildung 6 zu sehen ist. Die schrittweise Vererbung der Tonbeziehungen von Akkord zu Akkord ist offensichtlich unverträglich mit der Beobachtung (1), nach der die Tonorte des ersten Akkords mit denen des letzten übereinstimmen. Das  Töne-Noten-Problem kann sich demnach immer dann ergeben, wenn man in einer Partitur Quint- und Terzbeziehungen finden und miteinander verknüpfen will, obwohl die Notenschrift die Unterscheidung dieser beiden Arten der Tonbeziehung nicht unterstützt. 

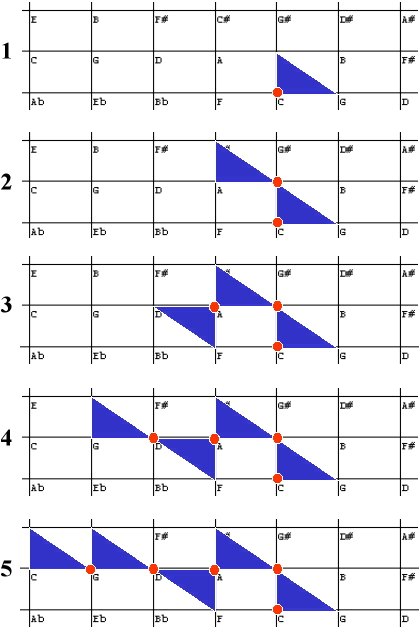
Abbildung 6: Riemanns Dreiklangsfolge im Eulernetz. In jeder der fünf Abbildungen kommt ein weiteres Akkord-Dreieck hinzu. Der Punkt in der obersten Abbildung markiert den Tonort C des ersten C-Dur-Dreiklangs. Die weiteren Punkte markieren jeweils die gemeinsamen Tonorte aufeinanderfolgender Akkorde. Unverträglichkeit mit Beobachtung (1): Der Eröffnungs-C-Dur-Dreiklang und der Schluß-C-Dur-Dreiklang haben verschiedene Tonorte. 

Welche Auswege gibt es aus dem Problem? Erstens könnte man das Eulernetz einfach verwerfen und mit ihm die Raummetapher des Tondenkens. Aber wollen wir gleich das Kind mit dem Bade ausschütten? 
Zunächst könnten wir überprüfen, ob nicht Hugo Riemann mit seinem konstruierten Beispiel an der musikalischen Praxis vorbeigeht. Schließlich könnte es ja sein, daß derartige konkurrierende Tonbeziehungen zwar theoretisch möglich sind, daß sie die Komponisten aber vermeiden, um unserem Tondenken keine Schwierigkeiten zu bereiten [8]. Doch das Gegenteil ist der Fall: Sie tun es auf Schritt und Tritt, und man könnte geradezu auf den Gedanken kommen, daß darin ein besonderer Reiz des Komponierens besteht. Eine ganz ähnliche Akkordfolge findet Ihr gleich zu Beginn des bekannten Präludiums in C-Dur aus dem Wohltemperierten Klavier - Teil I von Johann Sebastian Bach. Das folgende Beispiel zeigt die Noten der ersten acht Takte in vereinfachter Form. Die ersten vier Takte weisen dasselbe Problem auf: Aufgrund der verbindenden Akkordtöne C (von Takt 1 zu Takt 2), D (von Takt 2 zu Takt 3) und G (von Takt 3 zu Takt 4) müßte der C-Dur-Dreiklang in Takt 4 ein anderer sein als in Takt 1. Andererseits kommt es uns aber so vor, als würden wir zum selben Dreiklang zurückkehren. Ebenso spannend sind die nächsten vier Takte, wo sich abermals das Töne-Noten-Problem zeigt: 

Abbildung 7: Reduzierte Notation der ersten acht Takte des Präludiums in C-Dur aus dem Wohltemperierten Klavier - Teil I von Johann Sebastian Bach.

Der Tonort E- der Oberstimme in Takt 5 steht in Terzbeziehung zum Tonort C der Baßstimme. Von dort aus macht die Oberstimme vier Quartschritte (bzw. Quintschritte in umgekehrter Richtung von rechts nach links im Tonnetz). Nach diesen vier Schritten erreicht die Oberstimme einen Tonort, der ebenfalls mit dem Tonort C zusammenfallen sollte. Im Eulernetz ist dies aber wiederum nicht möglich. Entweder kann einer der vier Schritte keine gewöhnliche Quarte sein oder aber die Verknüpfung der vier Schritte keine Terz. Kurzum: Von einer Vermeidung solcher Konflikte kann keine Rede sein. 
Welche anderen Auswege sind denkbar? Ein verbreitetes Konzept, das im Falle der sogenannten dur-moll-tonalen Musik eine Hilfe anzubieten scheint, ist die Dur-Tonleiter (bzw. die Moll-Tonleitern). Einige Theoretiker ordnen den sieben Noten der Dur-Tonleiter im Eulernetz feste Tonorte zu. Damit übertragen sie den Begriff der Tonleiter (oder Skala) buchstäblich aus dem Bereich der Noten in den der Tonorte. Im Falle der C-Dur-Tonleiter geht man dabei so vor, daß man zum Tonort C die beiden Nachbarn F und G auf der Quintachse hinzunimmt und sodann jeden dieser drei Tonorte als Grundton eines Dur-Dreiklangs auffaßt. Zu den drei Tonorten F, C und G kommen also noch die drei Tonorte A-, E- und B- jeweils in Terzrichtung hinzu, sowie der Tonort D von G aus in Quintrichtung. Damit hat man sieben Tonorte. Eine Konsequenz dieser Auffassung ist, daß den Noten D, F, A kein Moll-Dreiklang im Sinne eines Dreiecks von benachbarten Tonorten entsprechen kann. Das Problem ist der Tonort D, der zum Tonort A- nicht im Quintverhältnis steht (zu dem ja seinerseits der Tonort F in einem Terzverhältnis nach unten steht). Zu einem echten D-Moll-Dreiklang im Eulernetz fehlt der Tonort D-. Auch in der Rolle der beliebten (hinzugefügten) Sexte zum F-Dur-Dreiklang wäre dieser Tonort die plausible Wahl: 



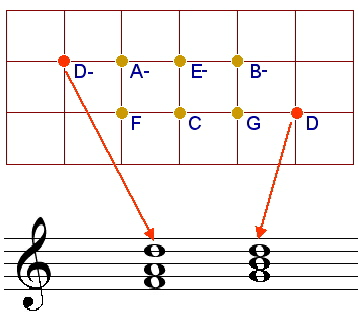
Abbildung 8: Zwei alternative Tonorte der Note D: D- als Tonort der Sexte im Sextakkord über F und als Quinte des G-Dur-Dreiklanges.

Die Entscheidung, ob man die Dur-Tonleiter im Eulernetz mit sieben oder jenen acht Tonorten modelliert, ist alles andere als harmlos! Das Eulernetz ist ein homoger Raum, d.h., es hat überall dieselbe Struktur. Dur- und Molldreiklänge sollten folglich auch überall dieselbe Dreiecks-Struktur haben, solange man keine Gründe für eine abweichende Auffassung vorbringt. Dies wäre ein Argument zugunsten der 8 Töne mit der Konsequenz, daß man das Töne-Noten-Problem hat: Wie ist es möglich, daß wir in unserem Tondenken scheinbar unmerklich vom Tonort D- zum Tonort D wechseln können? Wenn man die Raummetapher des Tondenkens ernst nimmt, dann ist das ein weiter Weg. Zwei Quintschritte sind mehr als einer, und erst recht sind 4 Quintschritte + 1 Terzschritt (nach unten) ein Weg, der dem Tondenken mehr auffallen sollte als beispielweise ein einziger Quintschritt. Sich dadurch aus der Affäre zu ziehen, daß man sich auf die kleine Tonhöhendifferenz des syntonischen Kommas beruft hieße anzunehmen, daß das Tondenken im Eulergitter ständig unterbrochen wird, um an anderen Stellen jeweils neu anzusetzen - ein ziemlich merkwürdiges Bild!  Andererseits: Mit einer festen Tonort-Skala, d.h. den sieben fixierten Tonorten hat man zwar das Töne-Noten-Problem nicht mehr, aber man gibt auch die tiefere Motivation für die Raum-Metapher des Denkens als ein Fortschreiten von Tonort zu Tonort auf, insofern man die Homogenität des Raumes mißachtet. Die Tatsache, daß dem D-Moll-Dreiklang in Riemanns Beispiel ein A-Dur-Dreiklang als Neben - Dominante vorangehen kann, zieht nach Riemanns Ansicht mit Notwendigkeit nach sich, daß wir uns den  D-Moll-Dreiklang als echten Moll-Dreiklang vorstellen. Das Modell einer festen Tonortskala zusammen mit dem falschen Moll-Dreiklang ruft eher die eingangs gegebene Assoziation einer zappelnden Kommode hervor, deren Schubladen die Skalentöne sind. 
Wir fassen zusammen: Will man die Raummetapher des Tondenkens anhand des Eulernetzes aufrechterhalten, so muß eine Erklärung dafür gefunden werden, wie es möglich ist, den weiten Weg von D- nach D scheinbar unmerklich zurückzulegen. Anders ausgedrückt: Wie ist es möglich, daß wir den Tonvektor von D- in Richtung des Tonorts D unbemerkt mit einer Prime verwechseln können? Wir nennen diesen Tonvektor, der sich aus 4 Quintvektoren und einem negativen Terzvektor zusammensetzt, im folgenden den syntonischen Tonvektor. Das Töne-Noten-Problem besteht also schlicht darin, daß der syntonische Vektor nicht der Nullvektor ist, und wir ihn (scheinbar) doch damit verwechseln können. Wie kann das sein? 

3 Das Noten-Tasten-Problem

Seit mehreren Jahrhunderten baut man Orgeln, Cembali, Klaviere, und andere Tasteninstrumente. Ungeachtet der vielen verschiedenen Arten, diese Instrumente zu stimmen, ist ihnen gemein, daß pro Oktave zwölf Tasten (oder) Pedale zur Verfügung stehen. Aus dem Paragraphen über das Töne-Noten-Problem wissen wir, daß sich das Notensystem in Richtung der B's und der Kreuze beliebig weit ausdehnen kann und in der Praxis immerhin 5 mal 7 = 35 Noten kennt. Folglich gibt es mehrere Noten, die jeweils mit derselben Taste gespielt werden müssen. Ein typisches Beispiel in der tonalen Umgebung von C-Dur/Moll sind die Noten Ab und G#: 

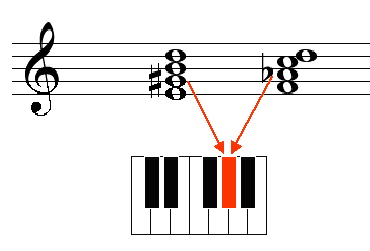
Abbildung 9: Zwei verschiedene Noten zur selben Taste: Gis und As

Man muß sich fragen: Warum baut man dann nicht Tasteninstrumente mit mehr Tasten? Diese Frage haben sich auch Theoretiker, Musiker und Instrumentenbauer immer wieder gestellt. Dabei wurden auch verschiedene Vorschläge gemacht und in die Tat umgesetzt. In den folgenden beiden Abbildungen seht Ihr eine Rekonstruktion des Archicembalos von Nicola Vicentino aus dem 16. Jahrhundert und ein Archiphon aus dem 20. Jahrhundert, das auf Ideen von Leonhard Euler zurückgeht. Solche Instrumente stehen jedoch vor allem im Museum und werden nur von ganz wenigen Enthusiasten in der Musikpraxis eingesetzt. Warum ist die Geschichte des Baus von Tasteninstrumenten nicht anders verlaufen? Handelt es sich hier um zufällige Entscheidungen, die dann aus Bequemlichkeit und wirtschaftlichen Günden beibehalten wurden? Zumindest ist die Frage berechtigt, ob sich in dieser Entwicklung nicht auch Spuren des Tondenkens finden lassen. Zwar haben wir eingangs gefordert, die Ebenen der Klangerzeugung, der Tonempfindung und des Tondenkens auseinanderzuhalten. Aber andererseits gibt es natürlich vermittelnde Transformationen zwischen diesen Ebenen. Eigentlich müßten doch Eigenschaften des Tondenkens geradezu Einfluß auf den Bau von Klangerzeugern haben. 

Abbildung 10: M.Tiella: Rekonstruktion des Archicembalo von Nicola Vicentino (1511-1576) (siehe http://www.infosys.it/pamparato/ima/ma/ma81/tastiere.html). 

Abbildung 11: Herman van der Horst: Archiphon (1970). Elektronische Version der von Adriaan Fokker gebauten Euler-Fokker-Orgeln von 1943 bzw. 1951 (siehe http://www.xs4all.nl/ huygensf/english/index.html). Im Zusammenhang mit der musiktheoretischen Untersuchung von Tasteninstrumenten spielt die Diskussion von Stimmungsfragen eine wichtige Rolle. 

Ein wichtiger historischer Entwicklungsschritt war die Einführung der wohltemperierten Stimmung in der ersten Hälfte des 18. Jahrhunderts. Johann Sebastian Bach hatte diese Entwicklung programmatisch befördert. Sein Zyklus Das Wohltemperierte Klavier zeigt, daß man von jedem Bezugston aus schöne Musikstücke komponieren und diese auf einem Tasteninstrument spielen kann.  Viele Theoretiker bezeichnen die wohltemperierten Stimmungen als akustischen Kompromiß. Dahinter steht die bereits eingangs erwähnte Annahme, daß den Tonbeziehungen ideale Frequenzverhältnisse der zu intonierenden Klänge entsprechen. Diese Charakterisierung mag in gewissem Sinne zutreffen, solange sie nicht mit der impliziten Annahme verbunden wird, daß eine Intonation in reinen [9] Intervallen kein Kompromiß sei. Nach dem, was wir aus dem Töne-Noten-Problem gelernt haben, muß jeder Versuch einer durchgängig korrekten reinen Intonation in der Musikpraxis zwangsläufig am Bestehen konkurrierender Tonbeziehungen scheitern. Die Zugeständnisse an die Intonation in wohltemperierter Stimmung bestehen also eher darin, daß der Spieler nicht in der Lage ist, diese oder jene Tonbeziehung durch intonatorische Rhetorik hervorzuheben. Solange aber aus dem musikalischen Kontext immer klar ist, welche Note (oder gar welcher Tonort) beim Niederdrücken einer Taste gemeint ist, so ergibt sich aus dieser Mehrdeutigkeit auch kein Problem für das Tondenken. Aus dieser Sicht wäre die temperierte Stimmung vergleichbar mit einem Redner, der ein bißchen nuschelt. Solange wir verstehen, was er sagt, können wir damit leben. Das Noten-Tasten-Problem kommt erst ins Spiel, wenn die Musiker (vermeintlich) jenes Nuscheln absichtlich einsetzen, um das Tondenken gezielt aus der Bahn zu werfen, bzw. in bestimmte Bahnen zu lenken. Dies passiert beispielsweise, wenn eine Note Ab in eine Note G# verwandelt wird, ohne daß dabei die gemeinsame Taste neu angeschlagen werden muß. Musiktheoretiker sprechen bei solchen Verwandlungen von einer enharmonischen Verwechslung oder Identifikation. Das Notenbeispiel ist eine konstruierte Akkordfolge, die von C-Moll nach A-Moll wechselt und dabei zwischen dem dritten und dem vierten Akkord solch eine Verwechslung vornimmt. 

Einige Theoretiker haben noch um die Jahrhundertwende solche enharmonischen Verwechslungen beargwöhnt und sie wie Rechtschreibfehler oder grammatische Fehler in der Sprache kritisiert. Als einen Rechtschreibfehler würde man die Verwendung der Note Ab ankreiden, wenn eigentlich doch G# gemeint ist und als einen (vermeintlichen) grammatischen Fehler die ernstgemeinte direkte Verwandlung von Ab in G#. Die Verwandlung im Notenbeispiel ist deshalb ernst gemeint, weil die Note C im ersten und letzten Akkord dieselbe sein soll. In der klassischen und romantischen Musik und später im Jazz erfreuten sich solche Verwechslungen zunehmender Beliebtheit (für eine Beispielsammlung siehe [L1]), und sie beschränkten sich keineswegs nur auf die Klaviermusik. In der romantischen Musik gibt es ein Phänomen, daß man als harmonische Rückung bezeichnet. Lustig ist an diesem Begriff in unserem Zusammenhang, daß er sich sowohl auf die Raummetapher des Tondenkens als auch auf die (zappelnde) Kommode beziehen lässt.   

Abbildung 12: Umdeutung von As in G# beim Übergang von c-moll nach a-moll.

Denn bei einer Rückung geht es nicht nur um einzelne Tonbeziehungen, sondern um ein ganzes Gefüge von Tonbeziehungen, das durch Verschiebung zu einem analogen Gefüge in Beziehung gesetzt wird. 

Wir betrachten zwei Beispiele mehrfacher harmonischer Rückungen, die verbunden mit einer Rückkehr zum Ausgangspunkt ernstgemeinte enharmonische Verwechslungen beinhalten. Beide Beispiele haben zudem einen außermusikalischen Bezug, der ebenfalls mit der Metapher des Fortschreitens zu tun hat. 

Im Gesang der älteren Pilger aus Richard Wagners Oper Tannhäuser (Szene III) läßt der Komponist die Pilger zur Buße gen Rom und damit der Erlösung entgegenschreiten, indem er sie auch musikalisch in fortgesetzten Kleinterzrückungen durch den Tonraum schreiten lässt. 

Abbildung 13: Acht Takte aus dem "Gesang der älteren Pilger" von Richard Wagner

Die Kleinterzrückungen führen von E-moll und G-Moll und Bb-Moll immer weiter nach links in die b-Richtung des Notensystems. Nach der enharmonischen Verwechslung zwischen Takt 5 und 6 kehrt der Satz jedoch aus #-Richtung, von rechts, zum Ausgangspunkt zurück. Wie klnnen wir im Sinne der Raummetapher des Tondenkens von rechts kommen, wenn wir zuvor konsequent nach links fortgeschritten sind? [10] 
Wir betrachten noch ein jüngeres Musikbeispiel aus der Jazzharmonik, das ebenfalls eine ernstgemeinte enharmonische Verwechslung beinhaltet. Der Jazzmusiker John Coltrane hat 1959 ein Stück mit dem Namen Giant Steps komponiert, in welchem das tonale Zentrum in rasantem Tempo in großen Terzen immer weiterrückt [11]. Die sich dabei einstellende Empfindung einer Rückkehr nach drei Terzschritten hängt wesentlich vom Stattfinden einer enharmonischen Verwechslung ab. 

Abbildung 14: Die ersten sieben Takte aus dem Jazzstück "Giant Steps" von John Coltrane 

Das Stück wandert in Großterzschritten von B (Takt 1) über G (Takt 2) nach Eb (Takt 3). In Takt 4 wird nochmal etwas Anlauf genommen, um die gleiche Schrittfolge eine Terz tiefer zu wiederholen. Folglich müßte es von G (Takt 5) über Eb (Takt 6) nach Cb  wandern (Takt sieben). Stattdessen stellt sich aber die Überraschung einer Rückkehr zum Ausgangspunkt ein. 
Im Rahmen dieses Aufsatzes geht es jedoch um die rein musiktheoretische Relevanz der Raummetapher des Tondenkens und hier konkret um eine möglichst präzise Formulierung des Noten-Tasten-Problems. Anhand der beiden Musikbeispiele wird klar, daß es sich bei der enharmonischen Identifikation eigentlich nicht um ein spezielles Phänomen der Musik auf temperiert gestimmten Tasteninstrumenten handelt. Indes werden wir in der Vermutung bestärkt, daß die Bevorzugung von Tasteninstrumenten mit 12 Tasten pro Oktave tiefere Gründe im Tondenken hat [12]. Insofern bezieht sich die Bezeichnung NotenTasten-Problem eher auf die oberflächliche Erscheinung eines Problems, als auf das Problem selbst. Wenn es sich bei der enharmonischen Identifikation jedoch um ein Phänomen des Tondenkens im Sinne der Raummetapher handeln soll, so kommen wir nicht umhin, die Ebene der Noten zu verlassen und zu Tonorten überzugehen. Ein solcher Versuch wird seinerseits durch das an dieser Stelle noch ungelöste Töne-Noten-Problem erschwert, aber wir versuchen eine möglichst einfache Formulierung: Der Weg von der Note Ab zur Note G# setzt sich aus drei Terzen zusammen. Obwohl unser konkretes konstruiertes Notenbeispiel eher zwei verschiedene Tonorte für die Note Ab (im zweiten und im dritten Akkord) nahelegt, wollen wir einfach annehmen, daß bei der enharmonischen Indentifikation im Eulernetz ein Weg von 3 Terzschritten (nach oben) zurückgelegt wird: Vom Tonort Ab+ zum Tonort C zum Tonort E- zum Tonort G# - -. Wir stehen vor der Frage, wie es möglich ist, daß wir in unserem Tondenken eine Identifikation von Tonorten vornehmen können, obwohl dabei eigentlich drei Terzschritte zu überwinden sein müßten. Auch hier gilt das einfache Argument: Zwei Terzschritte sind mehr als einer und drei sind mehr als zwei. Das Argument der kleinen Tonhöhendifferenz soll auch hier keine Berücksichtung finden, weil abermals das merkwürdige Bild eines Tondenkens entstehen würde, das bei jeder enharmonischen Identifikation in zusammenhangslose Fragmente zerfallen würde. Uns sollte ebenfalls die Zuückhaltung der strengen Theoretiker gegenüber der enharmonischen Verwechslung zu denken geben. In Lehrbüchern der Harmonielehre mögen einerseits didaktische Gründe eine Rolle gespielt ha- ben. Andererseits scheint die Identifikation des syntonischen Tonvektors mit einer Prime (d.h. das Töne-Noten-Problem) harmloser zu sein als die enharmonische Identifikation der Tonorte Ab und G#. Ein Überraschungseffekt ist offenbar Teil des Phänomens. Anlaß für die Formulierung des Noten-Tasten-Problems ist aber die Beobachtung, daß das Tondenken in allen drei Beipielen nicht aus der Bahn geworfen wird, obwohl das Modell der Fortschreitung im Tonnetz keinerlei Anhaltspunkt liefert, wieso das nicht passiert. Wir schlagen daher folgende Formulierung des Noten-Tasten-Problems vor: Wie ist es möglich, daß das Tondenken beim Fortschreiten im Tonnetz überraschenderweise an einen Tonort zurückkehrt, von dem es sich im Sinne seines Planes um drei Terzen entfernt haben sollte. Das Noten-Tasten-Problem gleicht der Suche nach einer unendlichen und zugleich zyklischen Treppe im Eulernetz nach der Art wie sie der niederländische Graphiker Maurits Cornelis Escher gezeichnet hat.

4 Quinten und Leitquarten - ein musikalisches Scrabblespiel

Unsere drei Beispiele von Bach (1722), Wagner (1845), und Coltrane (1959) liegen jeweils mehr als einen Jahrhundertschritt auseinander. Trotz erheblicher Unterschiede in der jeweiligen Auswahl und Verwendung von Tonbeziehungen ist es nicht von vornherein ausgeschlossen, daß sich ein gemeinsames Prinzip des Erschließens von Tonbeziehungen in einem geeigneten mathematischen Modell formulieren läßt. Ein solcher Versuch ist Gegenstand der Abschnitte 5, 6 und 7 dieses Aufsatzes. Dabei werden sich das Töne-Noten-Problem und das Noten-Tasten-Problem (bzw. deren Lösungen) als zwei Seiten einundderselben Medaille erweisen.

Abbildung 15: Unendliche Treppe von M.C. Escher: Gleicht das Tondenken in John Coltranes Stück "Giant Steps" dem Fortschreiten auf einer solchen zyklischen Treppe? 

Wenn man versucht, das Problem nach der Art zu lösen, wie das in besagten Abschnitten vorgeführt wird, so merkt man nach längerem Knobeln, daß ein ganz bestimmter mathematischer Trick angewendet werden muß, sonst gehen die Rechnungen einfach nicht auf. Dieser Trick hat allerdings weitreichende Konsequenzen für die musiktheoretische Interpretation des mathematischen Modells. Es ist deshalb sinnvoll, diese Konsequenzen schon vorbereitend anzudeuten [13]. 
Das Eulernetz wird von den Quinten und den Terzen als elementaren Intervallen oder Tonvektoren aufgespannt. Ihre besondere Rolle als elementare Intervalle verdanken sie bislang den einfachen Frequenzverhältnissen 3/2 und 5/4. Dieses Kriterium ist historisch für die Einführung des Eulernetzes wichtig gewesen. Im Zusammenhang mit dem Tondenken muß man auch folgende Argumente in Betracht ziehen. 

Die physikalischen Tonklänge der Musikpraxis weichen durchaus von idealen Frequenzverhältnissen ab und die Tonhöhenempfindung beinhaltet bereits Kategorisierungsleistungen. Wenn nun mit diesen Tonhöhenempfindungen ein aktives Denken in Tonorten interagieren sollte, dann gibt es ohne Weiteres keinen Grund für die Annahme, daß den Tonort-Beziehungen abermals Schwingungen zugrunde liegen sollten.

Begründet man die Mehrdimensionalität des Tonraumes mit der Unabhängigkeit der Primzahlen 3 und 5, so gibt es keinen Grund, warum nicht auch die Primzahlen 7, 11, 13 etc. Anlaß zu neuen Dimensionen des Tonraumes geben sollten. Es hat in der Musiktheorie nicht an Versuchen gemangelt, diesem Argument nachzugehen. Während sich für die Erforschung und Erfindung von Klangfarben in der Musik des 20. Jahrhunderts sehr anregende Impulse ergaben, haben sich daraus für die Erforschung von Tonbeziehungen bislang keine neuen Erkenntnisse ergeben.

Worauf wollen wir mit diesen Argumenten hinaus? Einerseits ist es legitim, ein Tonraum-Modell wie das Eulernetz ernst zu nehmen und damit zu experimentieren, ohne dogmatisch an jedem Detail zu kleben, das für seine Entstehung wichtig gewesen sein mag. Andererseits ist die Betrachtung der rationalen Frequenzverhältnisse seit der Antike ein zentraler Bestandteil der Musiktheorie gewesen, den man nicht ohne triftigen Grund über Bord wirft. Kurzum, wir verfolgen zwei Strategien: Einerseits halten wir es für möglich, daß die Betrachtung von Frequenzverhältnissen ein ungeeigneter Ansatz für die Untersuchung des Tondenkens ist, und andererseits halten wir im Verlauf der Untersuchungen trotzdem die Augen (und Ohren) offen, um uns interessante Beobachtungen nicht entgehen zu lassen. 
Worin besteht nun der besagte mathematischen Trick? Das Problem mit Quinte und Terz ist, daß sie ein ungleiches Paar sind. Für unser modifiziertes mathematisches Modell benötigen wir ein Paar von einander gleichenden Vektoren. Sie müssen in ihrer Rolle für das Tondenken ebenbürtig sein, d.h., ein Schritt in die eine Richtung muß in seiner musikalischen Wichtigkeit von derselben Qualität sein, wie ein Schritt in die andere Richtung. 
In erster Instanz wählt man die Quinte q als elementaren Tonvektor. Ihr ebenbürtig ist die Quarte -q, und in diesem Sinne nennen wir auch die Quarte einen quintartigen Tonvektor. Aber die Quarte liegt auf derselben Achse wie die Quinte und zeigt lediglich in die entgegengesetzte Richtung. Die Summe von Quinte und Quarte ergibt den Nullvektor:

q + -q = 0.

Erinnern wir uns nun: Das Töne-Noten-Problem besteht darin, daß der syntonische Tonvektor s nicht der Nullvektor ist, und wir ihn dennoch (scheinbar) damit verwechseln. Damit ist im Modell das zweite Elementarintervall, die Leitquarte p geboren: 

q + p = s.

Hierbei werden zwei zentrale Entscheidungen getroffen. Es wird ein zweites Quartintervall als elementarer Tonvektor eingeführt, welches im Eulernetz nicht mit der Quarte übereinstimmt und dennoch quintartig, d.h. der Quinte ebenbürtig ist. Darüberhinaus unterscheiden sich Quarte und Leitquarte genau um den syntonischen Tonvektor, der unser erstes Problem darstellt. Bevor wir uns von dem Nutzen überzeugen, den wir aus dieser Manipulation für die Lösung der beiden Probleme ziehen können, wollen wir die Leitquarte und ihr Umkehrintervall, die Leitquinte in musikalischer Hinsicht untersuchen. Die beiden Termini sind zunächst leere Namenshülsen. Was eine musiktheoretische Rechtfertigung verlangt, ist die Ablösung der Terz als einer elementaren Tonfortschreitung zugunsten der Leitquarte. Wie schon angedeutet, rechnen wir auch das zugehörige Frequenzverhältnis der Leitquarte aus: 

Eine erste Annäherung an eine musiktheoretische Rechfertigung der Leitquarte können wir aus der Beobachtung ziehen, die wir bei den Takten 5 bis 8 des Bach-Präludiums gemacht haben. Zur Erinnerung: In der Oberstimme kann entweder einer der vier Schritte keine gewöhnliche Quarte sein oder aber die Verknüpfung der vier Schritte keine Terz. Ein Ausweg bestünde darin, zugunsten der Terz einen der vier Quartschritte als Leitquartschritt zu interpretieren: 

Prinzipiell gibt es dazu vier Möglichkeiten. Wenn man den zweiten Schritt von der Note A nach zur Note D als Leitquarte (bzw. Leitquinte nach unten) aufzufasst, so entspricht dies gerade der einzigen Möglichkeit innerhalb der Tonort-Dur-Skala, die genau eine Leitquarte enthält, nämlich von A- nach D. 

A-	E-	B-
F	C	G	D

Die Terz (nach unten) läßt sich aus vier elementaren Schritten Leitquart + Quart + Quart + Quart zusammensetzen. Die Auffassung dieser Schritte als elementar wäre dann gerechtfertigt, wenn man den Melodieverlauf der Oberstimme mit demjenigen Weg in Verbindung bringen kann, den das Denken nehmen müßte, um die Terz zu verstehen. Terzen und Quarten gehörten aber in der Musikpraxis des 18. Jahrhunderts zum selbstverständlichen Grundvokabular, so daß aus praktischer Sicht die Frage nach einem elementaren Intervall sehr schwer zu entscheiden ist. Es kann sich deshalb als aufschlußreich erweisen, von dort aus zwei reichliche Jahrhundertschritte in die Vergangheit zu machen, um einige Begleiterscheinungen unter die Lupe zu nehmen, die mit der Emanzipation der Terzen im Kontrapunkt einhergingen. 
Bislang haben wir Fortschreitungen im Tonnetz als eine Art und Weise verstanden, nach der sich das Denken Tonbeziehungen erschließt. Dabei spielte es zunächst keine Rolle, ob alle beteiligten Tonorte tatsächlich komponierten Noten entsprechen, und wenn ja, ob diese dann gleichzeitig oder nacheinander erscheinen. In unseren Beispielen haben wir dabei keine systematische Differenzierung vorgenommen. 

In der mehrstimmigen Musik äußern sich Tonbeziehungen vordergündig auf zwei Weisen. In Anbetracht der Notenschrift kann man sie horizontale und vertikale nennen. Die horizontalen Beziehungen betreffen aufeinanderfolgende Noten bzw. Töne innerhalb einzelner Stimmen. Die vertikalen Beziehungen betreffen gleichzeitig erklingende Noten bzw. Töne aus verschiedenen Stimmen. Auf den ersten Blick gleicht also die mehrstimmige Musik einem Scrabble-Spiel. In der folgenden Abbildung sieht man links ein Buchstaben-Scrabble und rechts eine kleine zweistimmige Partitur. Die Wörter im Scrabble entsprechen dabei gebräuchlichen Namen der mit Strichen markierten horizontalen und vertikalen Tonbeziehungen [14]. 

Abbildung 16: Kontrapunkt als Scrabblespiel?

Auf den zweiten Blick merkt man jedoch, daß dieser Vergleich hinkt. Die Tonbeziehungen in der mehrstimmigen Musik sind nicht immer horizontal oder vertikal, sondern sie können auch um die Ecke gehen. Bei der Formulierung des Töne-Noten-Problems haben wir es als Selbstverständlichkeit angesehen, auch Tonbeziehungen um die Ecke zu lesen. Einerseits hatten wir liegenbleibende und wiederkehrende Töne berücksichtigt und andererseits die Tonbeziehungen innerhalb der Akkorde. Es gibt einen suggestiven Begriff in der Alten Musik, der eine problematische Konstellation auf den Punkt bringt, die beim Um-die-Ecke-Lesen auftreten kann: der Querstand. Damit meinen die Musiktheoretiker das dichte Aufeinanderfolgenden einer unalterierten und einer alterierten Variante desselben Stammtons in zwei Stimmen, z.B. B und Bb oder F und F#. Diese Tonbeziehungen gehen "quer"durch die Partitur. Damit ist jedenfalls klar, daß das Scrabble-Modell für den Kontrapunkt zu einfach ist [15]. 

Wir wollen nun das kleine Noten-Beispiel aus Abbildung 16 mit Tonorten des Eulernetzes interpretieren. Rechtfertigen läßt sich ein solcher Versuch aus der Kombination zweier Argumente:  

1. Die Emanzipation der Terzen und Sexten zu imperfekten Konsonanzen [16] legt das Eulernetz für die vertikalen Tonbeziehungen nahe. 

2. Die Tatsache, daß Tonbeziehungen im Kontrapunkt auch quer durch die Stimmen hergestellt werden, macht es erforderlich, daß alle Tonbeziehungen in einem gemeinsamen Tonraum hergestellt werden können.

Im Sinne des Arguments 1 sind die Tonbeziehungen, die den drei vertikalen Intervallen kleine Sexte B - G, große Sexte A - F # und Oktave G - G jeweils einzeln zuzuordnen sind, klar: Der Oktave entspricht zweimal derselbe Tonort, der kleinen Sexte entspicht ein Terzschritt nach unten und der großen Sexte entspricht ein Quartschritt plus ein Terzschritt. Es kommt also auf die Diskussion der horizontalen Tonbeziehungen an. In der Unterstimme, dem Tenor, bieten sich zwei Alternativen an: Zunächst ist für die Tonbeziehung vom A zum G ein doppelter Quartschritt sehr plausibel. Dies wird insbesondere bei der dreistimmigen Kadenz deutlich, die wir weiter unten betrachten. Aber der erste Tenorton B kann entweder als Terz inbezug auf den Schlußton gedeutet werden oder aber als doppelter Quartschritt zum nachfolgenden A. Im ersten Fall würden sich Tonbeziehungen nach der Art der Tonort-Dur-Skala ergeben, ganz wie beim Bachbeispiel. Insbesondere würde eine Leitquarte in die horizontale Beziehung von B nach A eingehen. Im zweiten Falle würde ein Töne-Noten-Problem entstehen, denn in der Oberstimme, dem Diskant, würden der ersten und dritten Note die verschiedenen Tonorte G- und G zukommen. Es gibt durchaus Argumente zugunsten der zweiten Auffassung. Erstens ist der Tenor die bestimmende Stimme im frühen Kontrapunkt. Zweitens war das Modell der pythagoräischen Skala, d.h. das einer Quintenkette für die Erklärung der melodischen Skalen, der Modi, sehr verbreitet. Drittens ergibt die folgende dreistimmige Version dieser Kadenz, daß die sogenannte Vorhaltsquarte zwischen Baß und Diskant sich als Leitquarte herausstellt. 


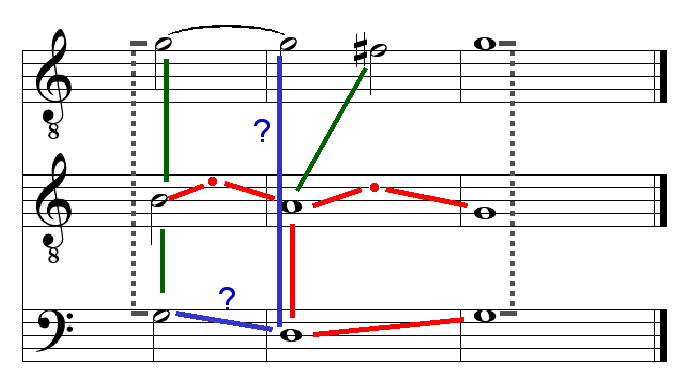
Abbildung 17: dreistimmige Kadenz: die Vorhaltsquarte zwischen Baß und Sopran erweist sich als Leitquarte, wenn der Tenor zwei pythagoräische Ganztonschritte macht. 

Hierzu muß angemerkt werden, daß es sich bei diesem Beipiel um eine typische Schlußbildung handelt, deren einzelne Bestandteile gleichermaßen zusammenspielen. Wenn es sich insbesondere um den sogenannten mixolydischen Modus handelt, bei dem der Ton F Stammton ist, muß dennoch in der Schlußbildung der erhöhte untere Leitton F# verwendet werden, der seinerseits daran gebunden ist, daß er Diskantton einer imperfekten Konsonanz ist, die von einer perfekten Konsonanz gefolgt wird. Diese Bedingungen haben zusammen immer zur Folge, daß ein Leitton von einer Quintgeraden des Eulernetzes in eine benachbarte hinüberleitet. Ebenso kann die Melodik des Diskants deswegen nicht ausschließlich pythagoräisch sein. Die Wahl der Termini Leitquarte und Leitquinte erhält durch diese Beobachtung ihre Berechtigung, denn auch diese Intervalle leiten von einer Quintgeraden in eine benachbarte.  

1. Die Vorhaltsquarte gilt als dissonant, da sie in die nachfolgende Terz aufgelöst werden muß [17]. Das Aufkommen der Akzidentien, d.h. der erhöhten oder erniedrigten Leittöne, die Emanzipation der Terzen und Sexten zu imperfekten Konsonanzen und das Aufkommen der dissonanten Quarte sind Prozesse, die in einem tieferen Zusammenhang stehen. Bei der Beantwortung der Frage, ob nicht viemehr die Leitquarten als elementare Schritte des Tondenkens in Frage kommen anstelle der Terzen, sollte man diese Sachverhalte berücksichtigen. Läßt man die beliebten rationalen Frequenzverhältnisse als Motivation mal außer Acht, so gibt es folgende Argumente zu bedenken:  Die Tatsache, daß es zwischen dissonanten Quarten und imperfekten Konsonanzen einen tieferen Zusammenhang gibt, laßt zumindest die Vermutung zu, daß sie im Tondenken eng miteinander zusammenhängen. Insofern macht es zumindest Sinn danach zu fragen, ob erstere vielleicht als elementare  Bestandteile der zweiteren eine Rolle spielen könnten. 

2.  Um eine Basis für das Eulernetzes zu bilden, kann neben der Quinte nur ein weiteres Intervall (und dessen Umkehrintervall) Berücksichtigung finden. Wenn man die große Terz dazu heranzieht, dann ist ihr Umkehrintervall - die kleine Sexte - ebenso elementar. Die kleine Sexte würde sich folglich als für das Tondenken elementarer erweisen müssen als die kleine Terz, was nicht sehr plausibel ist. 

3. Die Forderung nach möglichst natürlicher Verknüpfung von vertikalen mit horizontalen Tonbeziehungen legt die Auswahl eines ebenbürtigen quintartigen Tonvektors neben der Quinte selbst nahe. 

Wir schließen diesen Ausflug in musiktheoretische Erörterungen mit folgen der Bemerkung ab. Die Skepsis gegenüber einer eineindeutigen fixierten Zuordnung der Noten eines Modus zu Tonorten des Eulernetzes, die wir im Falle der Durtonleiter wegen des falschen D-Moll-Dreiklangs hegten, ist auch hier bei der Diskussion der Modi angebracht. Erinnern wir uns: Dort war es die Homogenität des Raumes, die gegen solch eine Auffassung sprach. Eine Schlüsselrolle könnten hier die Leittöne spielen. Die Verwendung der Akzidentien ist an ganz spezielle Situationen gebunden nach der Art der beiden Beispiele. Dies könnte ein Indiz dafür sein, daß auch in den Fällen, in denen der Leitton nicht erhöht oder erniedrigt werden muß, weil er schon die richtige Note hat, ihm dennoch ein anderer Tonort zukommt, als in den Situationen, wo er nicht zwecks Schlußbildung zur Finalis (dem Hauptton des Modus) geführt wird [18]. 

5 Das Rechnen im gekrümmten Tonraum

Das Eulernetz hat zwei Dimensionen. Die musikalisch ausgezeichneten Richtungen sind die ursprünglich Quint- und die Terzrichtung, bzw. nach unserer Modifikation die Quint- und die Leitquartrichtung. Von jedem Ton aus sind diese Richtungen dieselben, was daran liegt, daß das Eulergitter flach ist. Solange man in derselben Richtung fortschreitet, so verläuft der zurückgelegte Weg stets entlang von Geraden. Rechnerisch bedeutet dies, daß man von einem Tonort T = (a, b) startet und immer wieder denselben Vektor v = (s, t) addiert um zum nächsten Tonort zu gelangen. Wenn wir Quinte und Leitquarte als Basisrichtungen wählen, dann entspricht dem fortgesetzten Fortschreiten in Quintrichtung die k-malige Addition des Vektors (1, 0): 

(a, b), (a + 1, b), (a + 2, b), ..., (a + k, b)

Bei einer fortgesetzten Fortschreitung um eine große Terz addiert man k mal den Vektor (3, -1) 

(a, b), (a + 3, b - 1), (a + 6, b - 2), ..., (a + 3k, b - k)

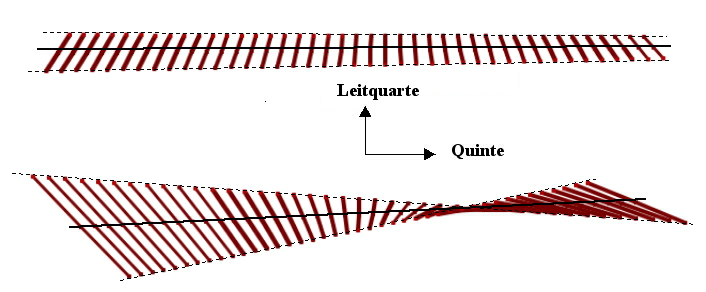
Wie die folgende Abbildung klarmacht, gibt es jedoch Räume, wo man sich zwar in einigen Richtungen auf Geraden fortschreiten kann, aber in anderen Richtungen sind die Wege die man bei Einhalten derselben Richtung zurücklegt, gekrümmt. Außerdem variieren die einander entsprechenden Richtungen von Punkt zu Punkt. Wie soll man das verstehen? Man denke sich ein Gitter aus Stäben, die man verlängern, verkürzen und in sich verdrehen kann, die jedoch immer gerade bleiben (so etwas wie Antennen von einem Kofferradio). Solange das Gitter flach ist, kann man in jedem Gitterpunkt dieselben beiden Richtungen identifizieren (z.B. nach rechts und nach hinten). Wenn man dann das Gitter im Raum verdreht, so kann man noch immer in jedem Punkt zwei Richtungen identifizieren und einander zuordnen, allerdings variieren sie von Punkt zu Punkt. (siehe Abbildung 18) 

Abbildung 18: Vom flachen zum gekrümmten Tonraum: Oben verläuft die Quintrichtung für jeden Gitterpunkt von links nach rechts und die Leitquartrichtung ist jeweils senkrecht dazu und ist für alle Gitterpunkte dieselbe. Wenn man das Gitter wie unten verdreht, dann variiert die Leitquartrichtung individuell für jeden Gitterpunkt. Dasselbe gilt für die Quintrichtung der mittleren Gitterlinie im Vergleich zu jenen der hinteren und vorderen Ränder des Gitters. Oben sind es drei parallele Geraden. Nach der Verdrehung sind es immer noch Geraden, aber sie haben unterschiedliche Richtungen. 

Wie soll man in solch einem Raum rechnen? Es ist ein bisschen komplizierter, aber nicht sehr. Zuerst sucht man sich einen flachen Umgebungsraum U, der unseren gekrümmten Raum S enthält. U hat mehr Dimensionen als S. Die Geraden im gekrümmten Raum sind dann ganz gewöhnliche Geraden im flachen Umgebungsraum. Da der Umgebungsraum aber nun auch Punkte enthält, die nicht zu unserem Teilraum S gehören, und wir diese auch nicht durch Fortschreitungen erreichen wollen, brauchen wir ein Kriterium, mit dem man überprüfen kann, ob ein Punkt zu S gehört oder nicht. Schließlich müssen wir für jeden Tonort T in S wissen, welches die Quintund welches die Leitquartrichtung ist. Dies sind Vektoren q_T und p_T im Umgebungsraum U, deren Koordinaten, von T abhängen. Ein Schritt von T aus in Quintrichtung führt dann zum Tonort T + q_T und in Leitquartrichtung zum Tonort T + p_T .
Die Ortsabhängigkeit der beiden Richtungen wird im Verborgenen durch die Raumkrümmung kontrolliert, auf die wir hier nicht eingehen. Aber insbesondere gilt folgendes: Die Quintrichtung im Tonort T + q_T muß dieselbe sein wie in T , nämlich q_T. Analog gilt für die Leitquartrichtung in T + p_T, daß sie mit derjenigen in T übereinstimmt. D.h. solange wir beim fortgesetzten Fortschreiten die Richtung nicht wechseln, sollte sich auch diese Richtung selbst nicht ändern. Nach diesen Vorbemerkungen können wir die konkrete Situation unseres gekrümmten Tonraumes studieren: 

1. Unser Umgebungsraum U ist ein vierdimensionaler euklidischer Raum. Normalerweise schreibt man ja vierdimensionale Vektoren in der Form (a, b, c, d), wobei a, b, c, und d reelle Zahlen sind. In unserem Falle ist es angebracht, diese vier Zahlen in Form von 2 × 2-Matrizen zu schreiben: 

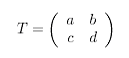
2. Die Bedingung dafür, daß T einen Punkt des gekrümmten Teilraumes S repräsentiert, ist das Erfülltsein der Gleichung 

ad - bc = 1.

3. Quint- und Leitquartvektor am Tonort T si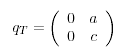nd 

und .

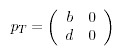Für die Rechnungen ist es sehr praktisch, eine Kurzschrift für die elementaren Tonfortschreitungen zu verwenden. Anstelle von T + q_T schreiben wir . Damit bezeichnen wir den Tonort, den wir von T aus mit einem Quintschritt erreichen.

 . 

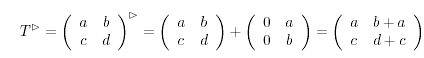Nun müssen wir überprüfen, ob die Quintfortschreitung überhaupt innerhalb des Raumes S möglich ist. Dazu muß das Kriterium von Punkt (2) für den Tonort überprüft werden: 

a(d + c) - (b + a)c = ad + ac - bc - ac = ad - bc = 1. 

Das heißt: Solange T in S liegt, liegt auch in S. 

Anstelle von T + p_T schreiben wir . Damit bezeichnen wir den Tonort, den wir von T aus mit einem Leitquartschritt erreichen.

 .

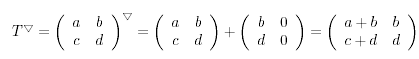Auch hier wir überprüfen wir, ob die Leitquartfortschreitung tatsächlich immer eine Fortschreitung innerhalb des Raumes S ist: 

(a + b)d - b(c + d) = ad + bd - bc - bd = ad - bc = 1.

Solange T in S liegt, liegt auch  in S.
Auch für die jeweils entgegengesetzten Fortschreitungen verwenden wir Kurzschreibweisen: bezeichnet den Tonort, den man von T aus mit einer Quartfortschreitung erreicht und bezeichnet den Tonort, den man von T aus mit einer Leitquintfortschreitung erreicht:

,
.

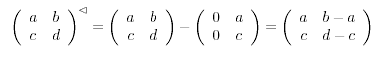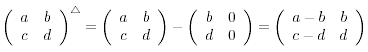Zum Abschluß dieses mathematischen Intermezzos errechnen wir eine Fortschreitung in zwei Schritten, bei der ein Richtungswechsel stattfindet. Von einem Tonort T aus berechnen wir den Tonort , den wir erreichen nach einem Quintschritt, der gefolgt wird von einem Leitquartschritt. 

.

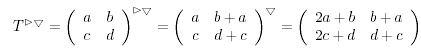6 Lösung des Töne-Noten-Problems

Erinnern wir uns: Das Töne-Noten-Problem besteht darin, eine Erklärung dafür zu finden, wie es möglich ist, daß das Tondenken scheinbar unmerklich die große Distanz zwischen den Tonorten D- und D zurückzulegen vermag. Diese Distanz muß im Eulernetz deswegen zurückgelegt werden, um in Riemanns Beispiel und ebenso in den ersten vier Takten des Bach-Präludiums eine Rückkehr zum Ausgangsdreiklang zu gewährleisten, wie sie von den Noten suggeriert wird. Dabei stellt sich zunächst die Frage, was es im Modell überhaupt bedeuten kann, daß eine Fortschreitung scheinbar unmerklich stattfindet. 
Als mögliche Fortschreitungen im gekrümmten Tonraum S haben wir in jedem Tonort T vier Möglichkeiten angegeben: man hat die beiden Basisrichtungen Quinte und Leitquarte, und deren Umkehrungen Quarte und Leitquinte. Wie die Abbildung zeigt, spannen beide Richtungen in jedem Tonort eine Tangentialebene auf [19]. Diese Tangentialebene ist so etwas, wie eine Kopie des vertrauten flachen Eulernetzes. 
Dieser Tangentialraum bietet uns eine zweite Möglichkeit des Rechnens an. Wir können Tangentialvektoren addieren. Am Ende des Abschnittes 5 haben wir eine Fortschreitung in zwei Schritten berechnet: Von D- einen Quintschritt nach und von dort einen Leitquartschritt nach . Es gibt natürlich auch im Ausgangstonort D- einen Leitquartvektor. Was bedeutet es, wenn wir zum Quintvektor in D- nicht den Leitquartvektor in A- addieren, wie es eigentlich sein muß, sondern den Leitquartvektor in D-? Die Tangentialvektoren in einem Tonort T kann man sich als FortschreitungsImpulse vorstellen, d.h. als Tendenzen des Tondenkens, in diese oder jene Richtung fortzuschreiten. Wenn man nun von einem Tonort aus bereits mehrere Schritte plant, so drückt die Summe der beteiligten Tangentialvektoren eine Gesamttendenz aus. Wir wollen das den scheinbaren Zieltonvektor eines solchen Fortschreitungsplans nennen. Am Beispiel des Fortschreitungsplans beträgt diese Gesamttendenz am Tonort 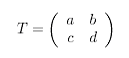beispielsweise .

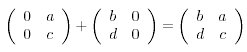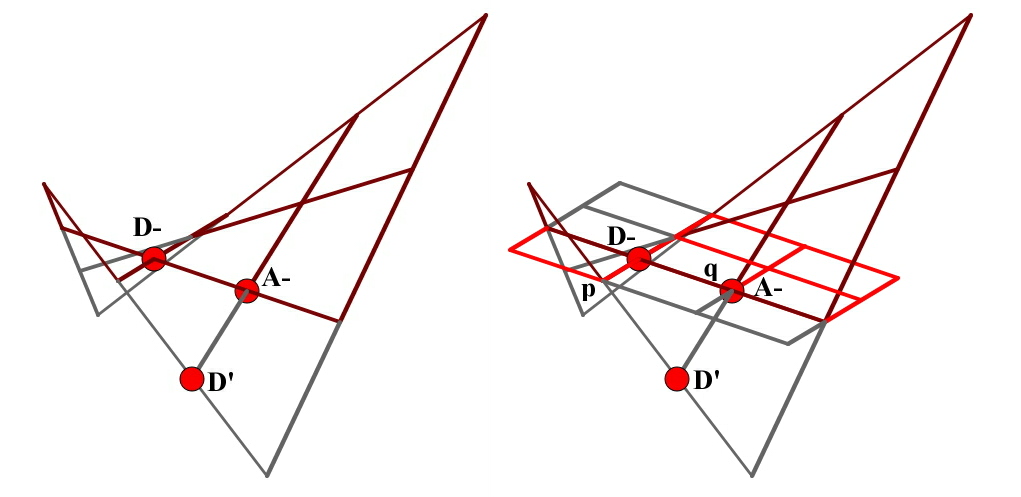
Abbildung 19: Links: Gekrümmter Tonraum mit 3 eingezeichneten Tonorten D-, und . Rechts: Im Tonort D- ist zusätzlich eine Tangentialebene eingezeichnet, die von Quinte und Leitquarte aufgespannt wird.

Wie können wir mit diesen Mitteln eine scheinbar unmerkliche Fortschreitung charakterisieren? Es liegt nahe, darunter solche Fortschreitungen zu verstehen, deren Gesamttendenz verschwindet, d.h. Fortschreitungen, die scheinbar an den Ausgangstonort zurückführen und deshalb einen zirkulären Fortschreitungsplan besitzen. Darin müssen genausoviele Quarten vorkommen, wie Quinten da sind, und es müssen genausoviele Leitquinten vorkommen, wie Quarten da sind. 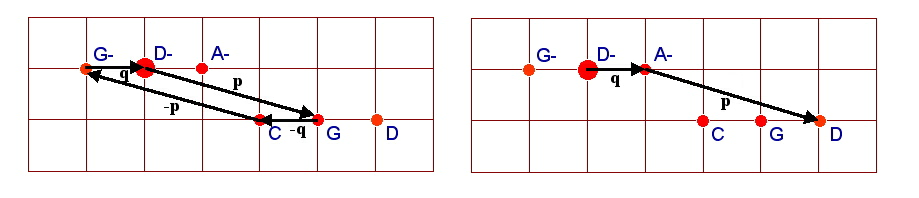Wir schauen uns einen solchen Fortschreitungsplan im Eulernetz an (siehe Abbildung): 
Den Ziel-Tonort, den wir beim rechten Fortschreitungsplan erreichen, haben wir bereits am Ende des Abschnitts 5 ausgerechnet: 

.

Die folgende Abbildung zeigt diese Fortschreitung im gekrümmten Tonraum, und dazu sehen wir vom Tonort D- aus abermals den Plan der scheinbar unmerklichen Fortschreitung im Tangentialraum des Tonorten D-: 

Abbildung 20: Zwei Fortschreitungspläne im Eulernetz, die vom problematischen Tonort D- ausgehen. Der linke Plan geht in zwei Schritten über das erwünschte G zum Grundton C unserer betrachten Akkordfolge und kehrt in weiteren zwei Schritten über das unerwünschte G- scheinbar zum Ausgangstonort D- zuück. Der rechte Plan nimmt stattdessen in zwei Schritten die erforderliche Korrektur vom D- zum D vor und zwar mit dem Umweg über A-. Dem linken Plan entspricht eine scheinbar unmerkliche Fortschreitung, während der rechte das Töne-Noten-Problem verkörpert. 

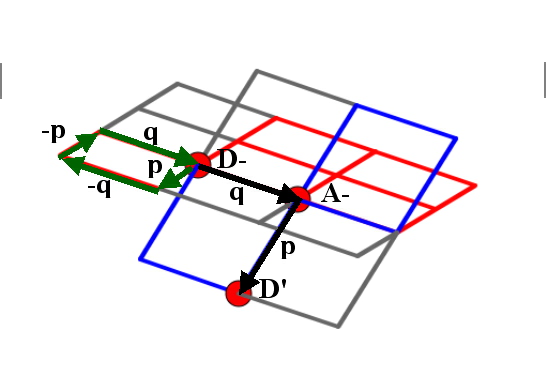
Abbildung 21: Die Fortschreitung Quinte-Leitquarte im gekrümmten Tonraum und der scheinbar unmerkliche Fortschreitungsplan p, -q, q, p vom selben Tonort aus. 

Nun rechnen wir den tatsächlichen Ziel-Tonort nach den vier Schritten aus:

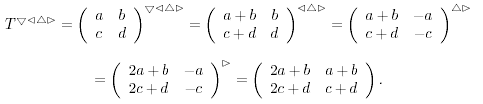
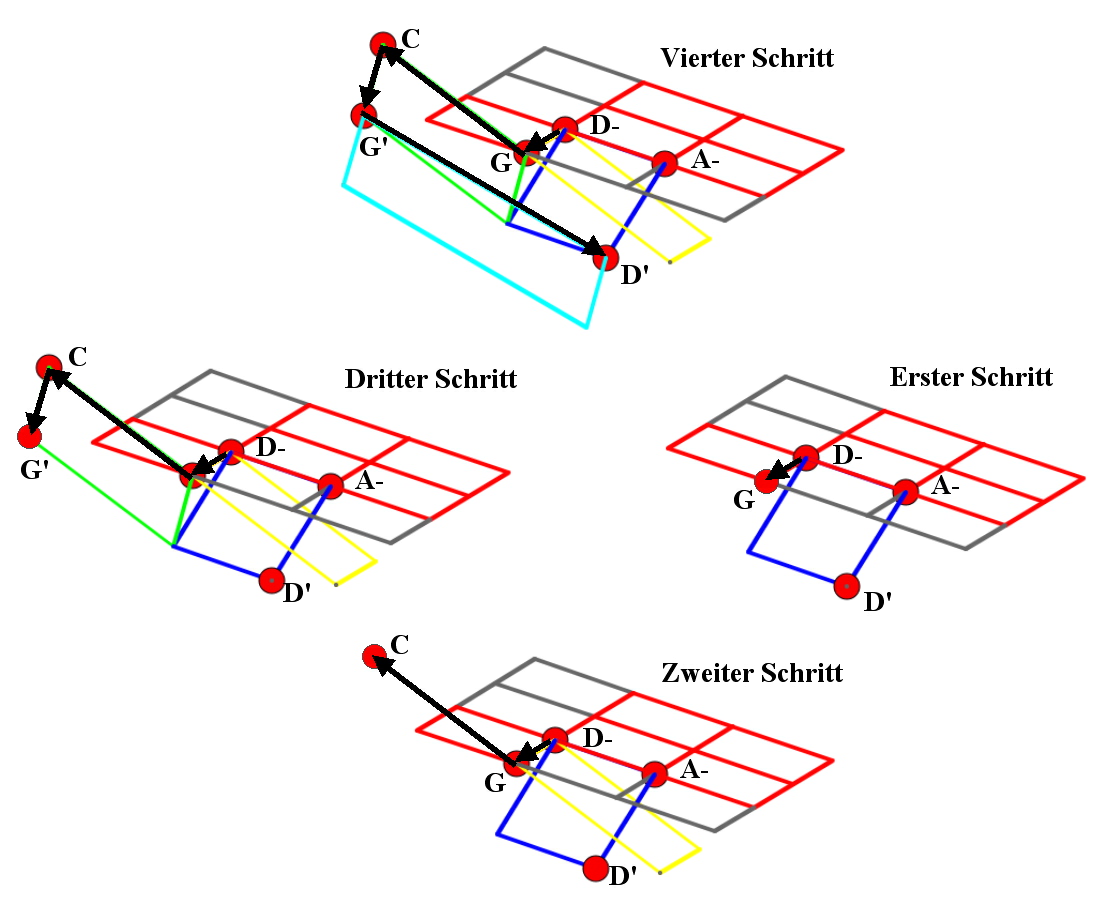
Abbildung 22: Scheinbare Rückkehr nach vier Schritten. Tatsächlich wird jedoch derselbe Tonort D' erreicht, den man auch in den zwei Schritten Quinte, gefolgt von der Leitquarte erreicht. 

Ein Vergleich der beiden Zieltonorte ergibt, daß beide Fortschreitungspläne zum selben Ziel-Tonort führen. Der erste verkörpert den syntonischen Tonvektor, denn seine Gesamttendenz ist q +p. Die Gesamttendenz des anderen hingegen ist der Nullvektor. Dies löst das Töne-Noten-Problem, denn der Vergleich der beiden Fortschreitungs-Pläne erklärt, wie wir scheinbar den syntonischen Tonvektor mit dem Nullvektor verwechseln können. 

7 Lösung des Noten-Tasten-Problems

Wie schon angedeutet, erweist sich im Rahmen des Modells vom gekrümmten Tonraum das Töne-Noten-Problem und das Noten-Tasten-Problem als zwei Seiten derselben Medaille. Unser Tondenken macht danach Pläne. Es antizipiert im Tangentialraum eines Ausgangstons seine eigene Geschichte im Voraus und kann sogar die Gesamttendenz bestimmen. Man kann sagen: Wir haben Denkimpulse. Darin gleicht das Modell dem flachen Eulernetz. Daneben schreitet es aber wirklich von Tonort zu Tonort fort. Im Falle des Töne-Noten-Problems gab es eine scheinbar unmerkliche Fortschreitung, die aber tatsächlich zu einem anderen Tonort führte. Was ist die Kehrseite dieser Medaille? Die Antwort ist ganz einfach: Das sind Fortschreitungen, die scheinbar woanders hinführen, aber tatsächlich zum Ausgangstonort zurückführen. Dies ist die Modellierung des Überraschungseffekts, der sich bei den enharmonischen Identifikationen einstellt. 
Nun müssen wir rechnen. Als Fortschreitungsplan kommt dabei eine dreifache Nacheinanderausfürung des Planes (q, q, q, -p) in Betracht: Drei Quinten und eine Leitquinte ergeben eine Terz nach oben. Um drei Terzen zu überwinden müssen wir folgende 12 Schritte machen: 

(q, q, q, -p, q, q, q, -p, q, q, q, -p). 

Der Zieltonvektor ist 9q - 3p. Und das ist verschieden vom Nullvektor.

 

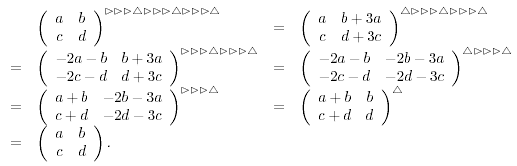
Wie wir sehen, kehren wir zum Ausgangs-Tonort zurück. 
Abschließend verfolgen wir noch einen anderen Fortschreitungsplan, der ebenfalls zum Ausgangs-Tonort zurückführt: 

(p, -q, p, -q, p, -q, p, -q, p, -q, p, -q).

Es handelt sich um einen wiederholten Wechsel von Quart- und Leitquartschritten, wie er etwa buchstäblich in den Grundtönen folgender II - V - Sequenz auftritt. . Sein scheinbarer Zieltonvektor ist 6p-6q. Hier nun die Rechnung: 

 

Abbildung 23: Enharmonische Identifikation

8 Schluß

Diese Überlegungen stellen einen Zusammenhang her zwischen einem mathematischen Modell und zwei musiktheoretischen Problemen, die darin gemeinsam gelöst werden und dadurch stärker aufeinander bezogen werden, als dies bislang getan wurde. Das mathematische Modell wurde hier allerdings nur angedeutet und die Musiktheorie ist voll von anderen interessanten Fragen, die nun ebenfalls zu neuen Antwortversuchen im Lichte des Modells einladen.

Literatur

[L1] Louis, R. und L. Thuille: Harmonielehre, Stuttgart, 1907. [zurück]

[L2] Mazzola, G.: Die Geometrie der Töne, Birkhäuser, Basel 1990.

[L3] Noll, T und A. Nestke: Die Apperzeption von Tönen, siehe
http://flp.cs.tu-berlin.de/noll).

[L4] Riemann, H.: Ideen zu einer Lehre von den Tonvorstellungen in: Jahrbuch der Musikbibliothek Peters 21/22, Leipzig 1914/15. 1-26.   [zurück]

Fußnoten

[0] Interdisziplinäre Forschungsgruppe KIT-MaMuTh für Mathematische Musiktheorie (http://www.mamuth.de) - finanziert durch die Volkswagen-Stiftung.  [zurück]

[1] Für eine weiterführende Lektüre siehe [L3] [zurück]

[2] Entstanden ist dieser Text anlässlich der Herbstschule Unerhörte Geometrie
siehe  http://www-sfb288.math.tu-berlin.de/vgp/unheard/ [zurück]

[3] Dazu gehören im Falle der hier diskutierten Fragen unbedingt Leonhard Euler  (1707 - 1783), nach dem das Eulernetz benannt ist, Hugo Riemann (1849 -      1919), der eine Theorie gefordert hat, nach der die Prinzipien des Vorstellens   von Tönen Grundlage der Musiktheorie sein sollten, und Guerino Mazzola, der vor etwa zwanzig Jahren damit begonnen hat, eine eigenständige Disziplin der Mathematischen Musiktheorie aufzubauen, die unter anderem von der Forderung ausgeht, die geometrischen Eigenschaften musikalischer Parameterräume ernstzunehmen. [zurück]

[4] Genauer gesagt: Bei Oktavidentifikation treten an die Stelle der Tonhöhen die sogenannten Tonigkeiten, d.h. Oktavklassen von Tonhöhen. [zurück]

[5] Dies ist die heutzutage verbreitetere Namensgebung. In der deutschsprachigen Tradition heißt dieser Ton H anstelle von B. Der Name B wird im Deutschen stattdessen für den Ton Bb benutzt. [zurück]

[6] Für die konkrete Wahl dieser Richtungen gibt es keine inhaltlichen Gründe. Insbesondere spielen auch Winkel keine Rolle. Es handelt sich lediglich um eine Gewohnheit, die von vielen Lehrbüchern beibehalten wird. [zurück]

[7] Die Bezeichnungen der Stimmen kennt man vom gemischten Chor: Sopran, Alt, Tenor und Baß. [zurück]

[8] Man müsste korrekterweise noch eine Verzweigung der Argumentation betrachten, die das Vermeiden einer vorhandenen Möglichkeit vom bloßen Nicht- der-Fall-Sein unterscheidet. [zurück]

[9] Damit sind die Intervalle im Sinne einfacher Frequenzverhältnisse gemeint, also 2:1, 3:2 und 5:4. [zurück]

[10] Zur (scheinbaren) Beruhigung des Innenministers: Dergleichen Fragen nach den ideologischen Rückungen führender Politiker sind nicht Gegenstand dieses Aufsatzes. [zurück]

[11] Die Schritte, auf die sich der Name des Stücks bezieht, sind die Kleinterz- und Quartschritte in der Baßstimme, die die Großterzrückungen unterteilen. [zurück]

[12] Der Komponist Hector Berlioz vergleicht in seiner Instrumentationslehre auch das romantische Orchester seiner Zeit mit einem temperierten Instrument. [zurück]

[13] Musiktheoretisch ungeschulte Leser könnten bei den Überlegungen dieses Abschnitts eventuell überfordert sein und diesen überspringen. [zurück]

[14] Ein Scrabble zu legen, ist manchmal knifflig, und in dem Beispiel wurde gemogelt: Zwischen Unterer und Leitton fehlt nämlich ein Zwischenraum. [zurück]

[15] Vielleicht kann ja der Kontrapunkt neue Regeln beim Scrabblespiel anregen:

	Möglichst viele Wörter, die man um die Ecke lesen kann, sollen einen Sinn ergeben.
	Nicht alle Wörter, die man horizontal legen kann, darf man vertikal legen und umgekehrt. [zurück]

[16] Als perfekte Konsonanzen gelten Einklang (Prime), Oktave und Quinte, als imperfekt gelten die Terzen und Sexten. [zurück]

[17] Kurioserweise würde das Frequenzverhältnis 27/ 20 der Leitquarte die Dissonanz dieses Vorhaltsintervalls auch aus der Perspektive der kleinen Zahlenverhältnisse rechtfertigen. Mir ist nicht bekannt, ob dieses Argument jemals angeführt wurde. Dieser Umstand muß sich ohnedies nicht auf die Intonation auswirken, denn die Vorbereitung der Vorhaltsquarte im Diskant sorgt hinreichend für das Herstellen der relevanten Tonbeziehungen. [zurück]

[18] Ähnliche Effekte kennt man von den verschiedenen Varianten der Molltonleiter. Wenn dieselbe Stufe sogar um einen Halbton variieren kann, dann sollte man die Variation um ein Komma erst recht für möglich erachten. [zurück]

[19] Zur Vereinfachung haben wir die dritte Dimension des Raumes S unterschlagen. [zurück]